Autocorrelation matrix
The autocorrelation matrix is used in various digital signal processing algorithms. It consists of elements of the discrete autocorrelation function, 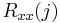 arranged in the following manner:
arranged in the following manner:
This is clearly a Hermitian matrix and a Toeplitz matrix. Furthermore, if 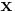 is a real valued function, then it is a circulant matrix since
is a real valued function, then it is a circulant matrix since 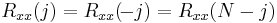 . Finally if
. Finally if 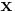 is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.
is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.
The autocovariance matrix is related to the autocorrelation matrix as follows:
Where 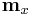 is a vector giving the mean of signal
is a vector giving the mean of signal 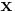 at each index of time.
at each index of time.
References
- Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
![\mathbf{R}_x = E[\mathbf{xx}^H] = \begin{bmatrix}
R_{xx}(0) & R^*_{xx}(1) & R^*_{xx}(2) & \cdots & R^*_{xx}(N-1) \\
R_{xx}(1) & R_{xx}(0) & R^*_{xx}(1) & \cdots & R^*_{xx}(N-2) \\
R_{xx}(2) & R_{xx}(1) & R_{xx}(0) & \cdots & R^*_{xx}(N-3) \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
R_{xx}(N-1) & R_{xx}(N-2) & R_{xx}(N-3) & \cdots & R_{xx}(0) \\
\end{bmatrix}](/2012-wikipedia_en_all_nopic_01_2012/I/498f2c9fb2efbc17bace83ff94d15128.png)
![\begin{align}
\mathbf{C}_x &= E[(\mathbf{x} - \mathbf{m}_x)(\mathbf{x} - \mathbf{m}_x)^H]\\
&= \mathbf{R}_x - \mathbf{m}_x\mathbf{m}_x^H\\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/35f2977d2119a256669b33591b853a74.png)